Daftar Pembahasan
PERSAMAAN NILAI MUTLAK

Apakah kalian sudah tau apa itu mutlak?
Mutlak dinotasikan dengan “| |” . Nilai mutlak suatu bilangan real x, dinyatakan dengan |x|, didefinisikan sebagai berikut ini:
|x| = x jika x ≥ 0
|x| = -x jika x < 0
Contohnya:
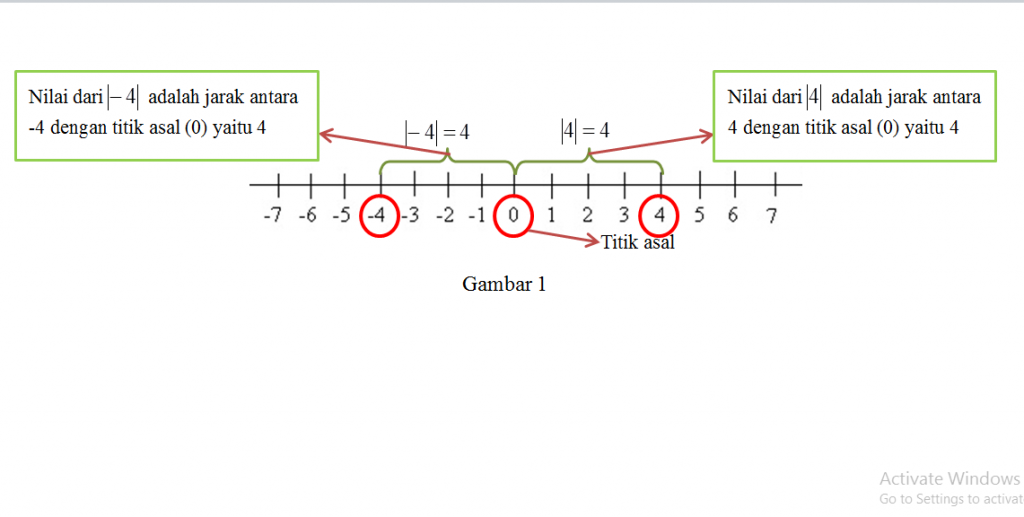
1. |4| hasilnya adalah 4 (positif) karena 4 ≥ 0.
2. |0| hasilnya adalah 0 karena 0 ≥ 0.
3. |-4| = – (-4) = 4 (jika dilihat menurut definisi -4 < 0 maka |-4| = – (-4) hasilnya adalah 4)
Definisi dari mutlak tidak mengatakan bahwa |-x| = x (bisa dilihat dan dipahami dari contoh x = -4). |x| atau “mutlak x” bisa di definisakan dengan “selalu tak negatif” dan benar bahwa |-x| = |x|.
-
Konsep Nilai Mutlak
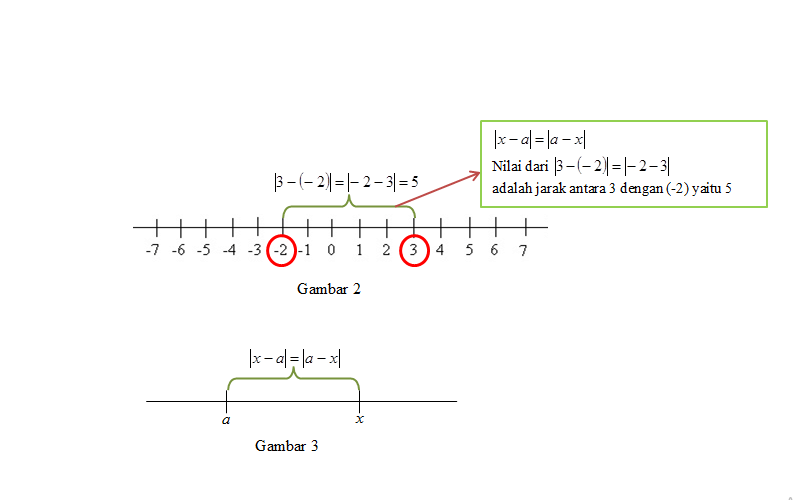
Jika kalian belum memahami apa itu nilai mutlak, kalian bisa membayangkan nilai mutlak sebagai jarak yang tidak berarah. Contohnya, |x | maka dapat diartikan dengan nilai mutlak dari x adalah jarak antara x dengan titik asal. Demikian pula untuk |x – a| adalah jarak antara x dan a. (dapat dilihat pada Gambar 1, Gambar 2, dan Gambar 3).
Sifat-sifat Nilai Mutlak

Sifat-sifat nilai mutlak pada persamaan nilai mutlak:
- |a| ≥ 0
- |-a| = |a|
- |a – b| = |b – a|
- |a| =
- |a|2 = a2
- Jika |a| < |b|, maka a2 < b2
- |ab| = |a||b|
- |a + b| = |a| + |b|
- |a – b| = ||a| – |b||
Contoh Soal dan Pembahasan Persamaan Nilai Mutlak
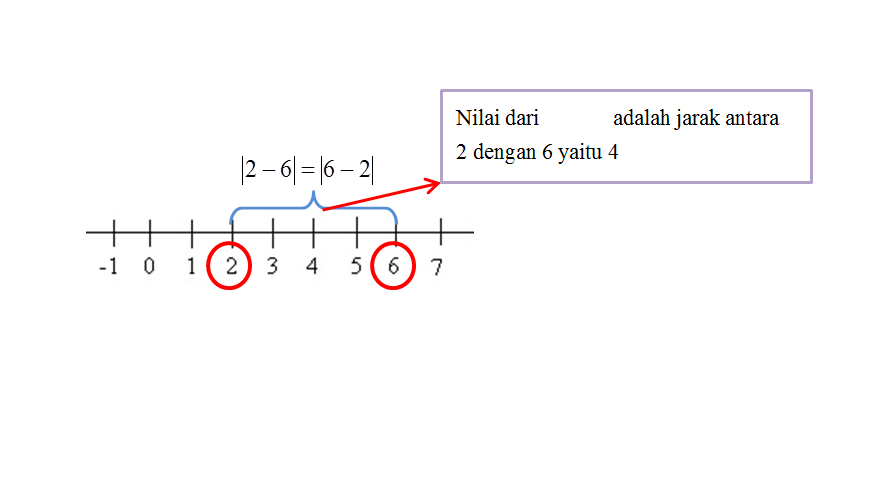
Contoh 1. Nilai dari |2 – 6| adalah …
Jawab :
|2 – 6| = |6 – 2| = |4| = 4
Penyelesaian dengan konsep jarak:
Contoh 2. Hitung nilai x pada persamaan |x – 7| = 12!
Jawab:
Berdasarkan definisi nilai mutlak ada dua kemungkinan nilai dari x, yaitu bernilai positif atau negatif
a. |x| = x jika x ≥ 0
x – 7 = 12
x = 12 + 7
x = 19
b. |x| = –x jika x < 0
-(x – 7) = 12
x – 7 = -12
x = -12 + 7
x = -5
Jadi, jawabannya adalah 19 atau -5.
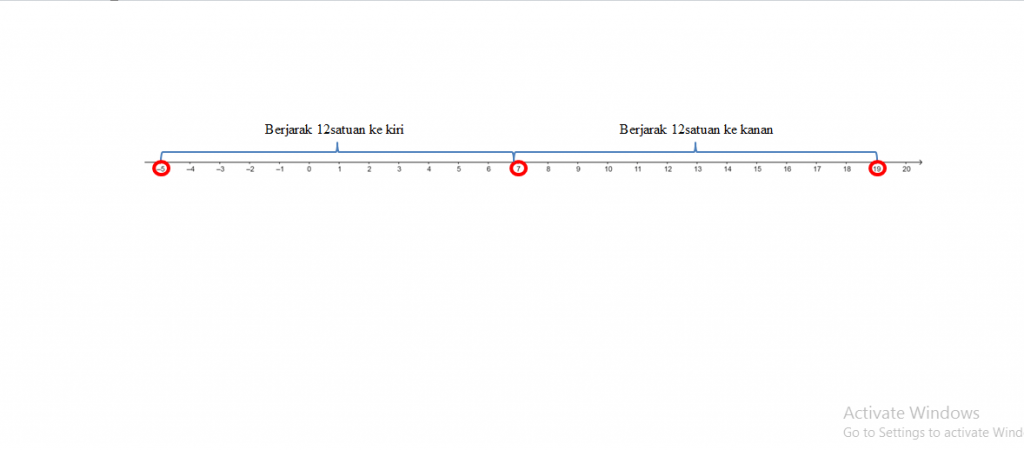
c. Jika menggunakan konsep jarak maka pertanyaannya menjadi: berapa nilai titik x yang berjarak 12 dari titik 7?
Titik yang berjarak 12 dari titik 7 adalah 19 atau -5.
Contoh 3. Hitung nilai x pada persamaan 2|x + 3|+5 = 15!
Jawab:
2|x + 3| + 5 = 15
2|x + 3| = 15 – 5
2|x + 3| = 10
|x + 3| =
|x + 3| = 5
Maka:
a. x + 3 = 5
x = 5 – 3
x = 2
b. – (x + 3) = 5
x + 3 = -5
x = -5 – 3
x = -8
Jadi nilai x adalah 2 atau -8
c. Dengan menggunakan konsep jarak, maka
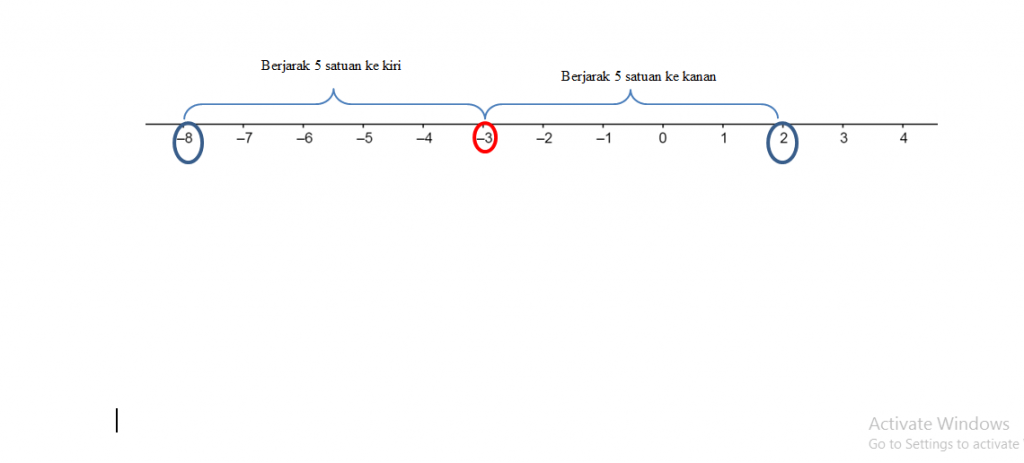
|x + 3| = 5 menjadi |x – (-3)| = 5
Jadi, berapa nilai titik x? Titik x berjarak 5 satuan dari (-3). Maka titik x adalah 2 atau -8.
Contoh 4. Selesaikan persamaan berikut |x + y| + |3x + 6| = 0!
Jawab:
Dari soal tersebut bisa dilihat bahwa |x + y| dan |3x + 6| bernilai positif. Apabila di jumlahkan kemungkinan hasilnya adalah nol (0) jika |x + y| bernilai 0 dan |3x + 6| juga bernilai 0. Maka,
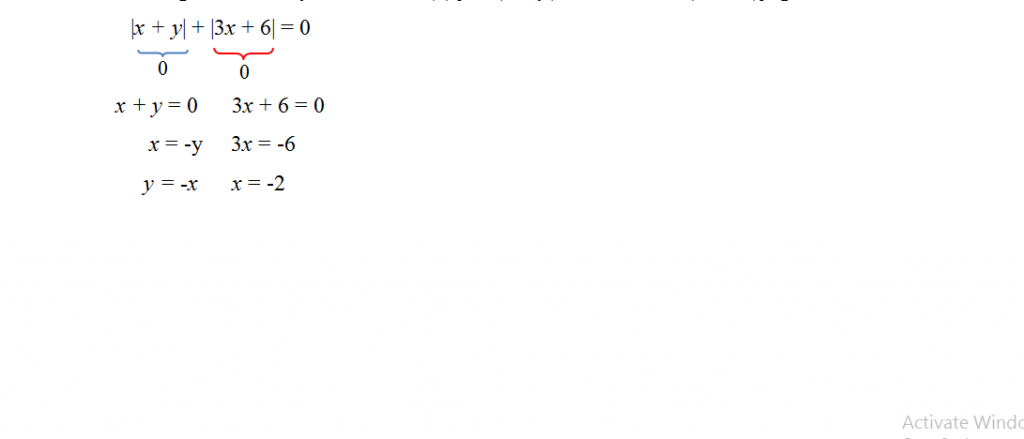
Substitusikan x ke y=-x untuk mencari nilai y
y = -x
y = –(-2)
y = 2
Hasilnya adalah x=-2 dan y=2.
B. Persamaan Nilai Mutlak Satu Variabel
Sifat-sifat persamaan linear mutlak satu variabel:
Untuk setiap a, b, c dan x bilangan real, maka
- Jika |ax + b| = c dengan c ≥ 0, maka berlaku sifat berikut:
- |ax + b| = c untuk x
- |ax + b| = c untuk x <
- Jika |ax + b| = c dengan c < 0 maka tidak ada bilangan real yang memenuhi persamaan
Contohnya:
Contoh 1. Tentukan nilai x yang memenuhi persamaan |3x + 1| = 10!
Jawab:
|3x + 1| = 10 dari persamaan tersebut dapat diketahui bahwa c = 10 yaitu ≥ 0, maka berlaku :
|3x + 1| bernilai 3x + 1 jika x ≥ atau bernilai –(3x + 1) jika x <
Dengan interval sebagai berikut:
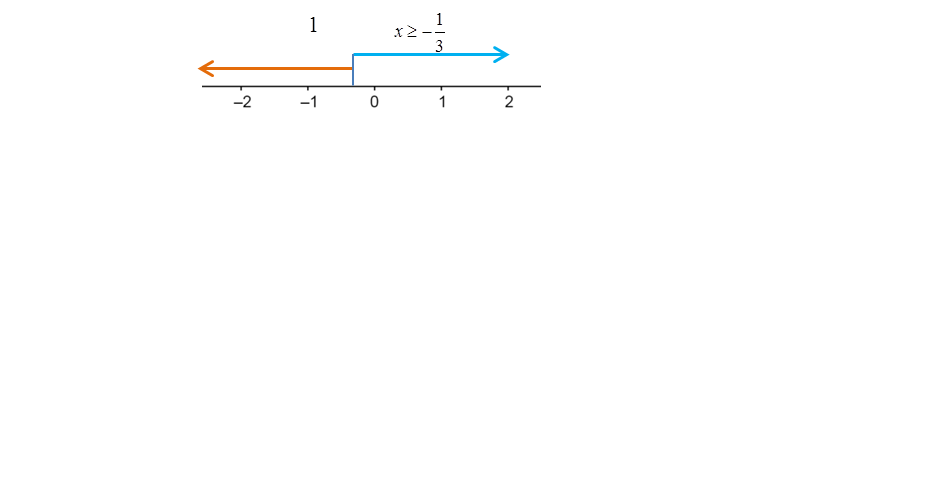
Sehingga diperoleh persamaan sebagai berikut:
a. Untuk x ≥ , maka
3x + 1 = 10
3x = 10 – 1
3x = 9
x = 9/3
x = 3
x = 3 memenuhi syarat x ≥ jadi x = 3 memenuhi.
b. Untuk x < , maka
-(3x + 1) = 10
3x + 1 = –10
3x = -10 – 1
3x = –11
x = -11/3
x = -11/3 memenuhi syarat x <
Jadi, nilai x yang memenuhi persamaan |3x + 1| = 10 adalah x = 3 atau x = -11/3.
Contoh 2. Tentukan nilai x yang memenuhi persamaan |2x – 4| + |x – 5| = 12!
Jawab:
Pertama, kita harus mencari batas-batas x dengan cara:
2x – 4 = 0
2x = 4 dan x – 5 = 0
x = 4/2 x = 5
x = 2
Dari persamaan |2x – 4| + |x – 5| = 12 dapat diketahui bahwa nilai c ≥ 0 yaitu 12, maka:
|2x – 4| bernilai 2x – 4 jika x ≥ 2 atau bernilai –(2x – 4) jika x < 2, dan
|x – 5| bernilai x – 5 jika x ≥ 5 atau bernilai –(x – 5) jika x < 5
Diperoleh interval sebagai berikut:
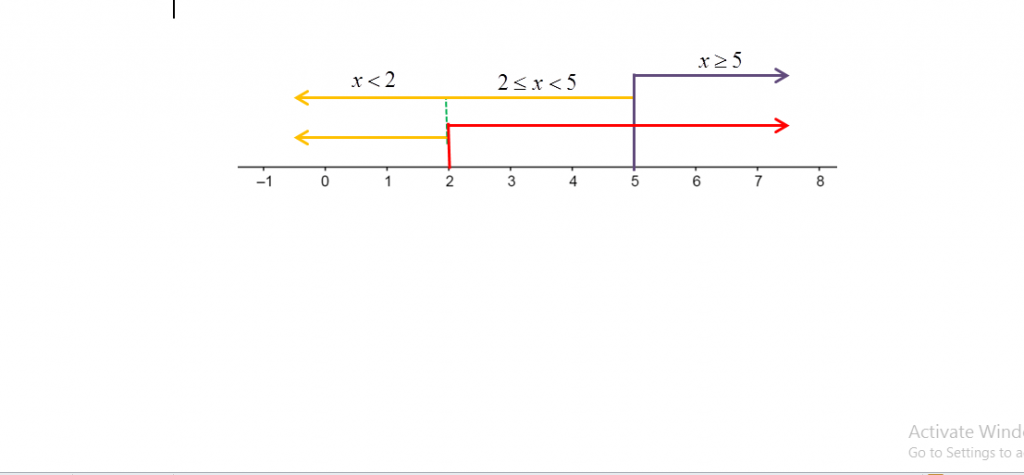
Sehingga persamaannya menjadi
a. Untuk x < 2
|2x – 4| + |x – 5| = 12 menjadi
-(2x – 4) + (-(x – 5)) = 12
-2x + 4 –x + 5 = 12
-3x + 9 = 12
-3x = 12 – 9
-3x = 3
x = -1
Memenuhi, karena x = -1 berada pada x < 2
b. Untuk 2 ≤ x < 5
|2x – 4| + |x – 5| = 12 menjadi
2x – 4 + (-(x – 5)) = 12
2x – 4 – x + 5 = 12
x + 1 = 12
x = 12 – 1
x = 11
Tidak memenuhi, karena x = 11 tidak berada pada interval 2 ≤ x < 5
c. Untuk x ≥ 5
|2x – 4| + |x – 5| = 12 menjadi
2x – 4 + (x – 5) = 12
3x -9 = 12
3x = 12 + 9
3x = 21
x = 21/3
x = 7
Memenuhi, karena x = 7 berada pada x ≥ 5
Jadi, nilai x yang memenuhi persamaan |2x – 4| + |x – 5| = 12 adalah x = 1 atau x = 7.
Contoh 3. Tentukan nilai x yang memenuhi persamaan |2x + 3| = -3!
Jawab:
Dari persamaan |2x + 3| = -3 dapat diketahui bahwa c < 0 maka tidak ada bilangan real yang memenuhi persamaan. Pembuktian:
|2x + 3| bernilai |2x + 3| jika x ≥ atau bernilai -|2x + 3| jika x <
Diperoleh interval sebagai berikut:
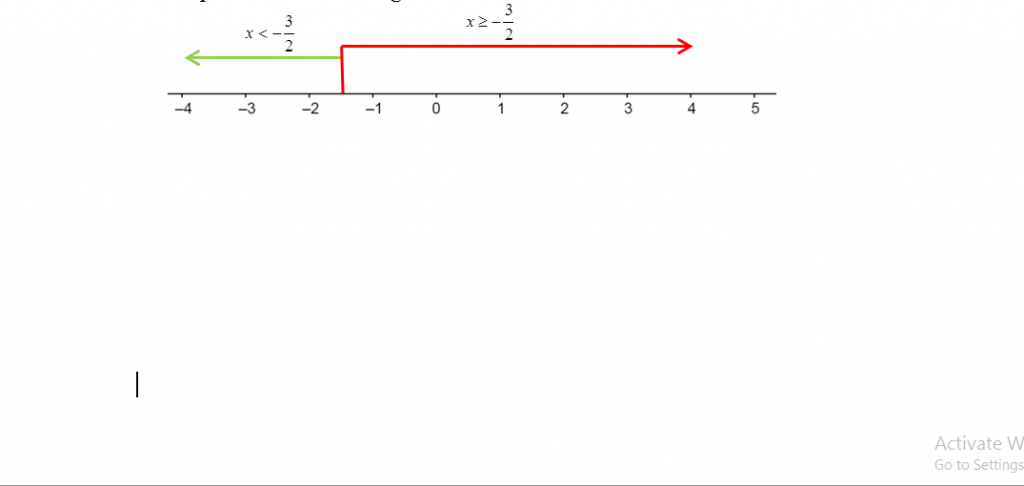
a. Untuk x ≥ ,
Maka, |2x + 3| menjadi
2x + 3 = -3
2x = -3 – 3
2x = -6
x = -6/2
x = -3
Tidak memenuhi, karena x = -3 tidak pada domain x ≥
b. Untuk x <
Maka, |2x + 3| menjadi
-(2x + 3) = -3
-2x – 3 = -3
-2x = -3 + 3
–2x = 0
x = 0
Tidak memenuhi, karena x = 0 tidak pada domain x <
Jadi, tidak ada nilai x yang memenuhi persamaan |2x + 3| = -3.