Daftar Pembahasan
TABUNG

Hallo semua sahabat setia syahrulanam.com pada kesempatan Kali ini akan kami bahas mengenai Rumus selimut tabung, pengertian tabung, ciri-ciri tabung, unsur-unsur tabung, contoh soal dan pembahasan yang kami rangkum dengan baaik dan mudah.
A. Pengertian Tabung
Tabung merupakan salah satu bangun ruang tiga dimensi dengan dua tutup yang terdiri dari dua lingkaran dengan ukuran yang sama dan sejajar dengan di selimuti oleh persegi panjang. Tabung juga merupakan bangun ruang sisi lengkung.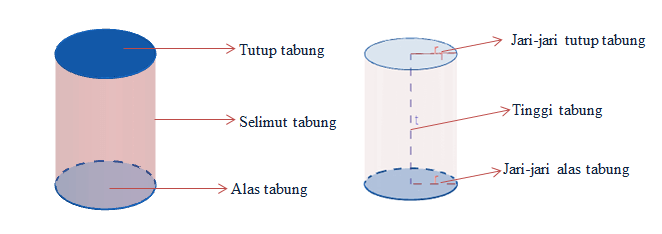
Perhatikan gambar di atas. Dari gambar tersebut dapat diketahui beberapa ciri-ciri tabung, antara lain:
1. Mempunyai alas dan tutup yang berbentuk lingkaran dengan jari-jari yang sama dan sejajar.
2. Mempunyai tiga sisi, yaitu alas tabung, tutup tabung, dan selimut tabung yang berbentuk persegi panjang.
3. Mempunyai rusuk yang berjumlah dua.
4. Tidak mempunyai titik sudut.
Apakah kalian sudah mengetahui kenapa kok selimut tabung berbentuk persegi? Kalau belum jelas bisa dilihat melalui gambar jaring-jaring tabung di bawah ini.
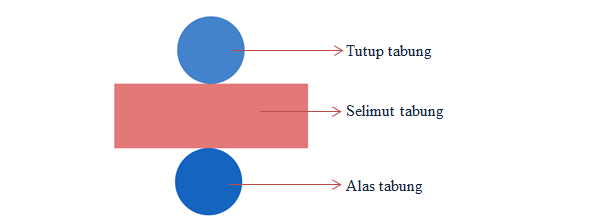
Nah, sudah jelas kan? Bisa dilihat bahwa selimut tabung berbentuk persegi panjang. Jika nanti persegi panjang tersebut di lingkarkan sesuai dengan keliling lingkaran maka akan membentuk selimut tabung. Panjang selimut sama dengan keliling dari alas atau tutup tabung. Lebar selimut sama dengan tinggi dari tabung yang sudah terbentuk.
B. Unsur-unsur Tabung
1. Tutup dan alas tabung ( tutup yang ada di bagian atas tabung sedangkan, alas tabung adalah bagian bawah dari tabung)
2. Selimut tabung ( selimut tabung adalah bagian yang mengelilingi tabung )
3. Rusuk tabung
C. Jenis Tabung dan Tabung dalam Kehidupan Sehari-hari
Jenis tabung ada dua, yaitu tabung tertutup dan tabung terbuka.
• Tabung tertutup adalah tabung yang mempunyai tutup dan alas atau seluruh sisinya tertutup.
• Tabung terbuka adalag tabung yang hanya mempunyai tutup atau hanya mempunyai alas atau tidak mempunyai alas dan tutup.
Apakah kalian bisa menyebutkan beberapa benda yang berbentuk tabung, baik tabung tertutup maupun terbuka?
Dalam kehidupan sehari-hari, benda yang berbentuk tabung sering kita temui. Misalnya gelas, pipa, botol minuman, kaleng kemasan, dan masih banyak lagi.
D. Rumus Tabung
1. Rumus Luas Permukaan Tabung
Setiap bangun ruang pasti mempunyai luas permukaan, begitu juga dengan tabung. Bagaimana cara menghitung luas permukaan? Luas permukaan dihitung dengan cara menghitung luas dari sisi-sisi yang membentuk bangun ruang tersebut yang kemudian di jumlahkan. Jadi, untuk menghitung luas permukaan tabung juga dengan menjumlahkan sisi-sisi yang membentuk tabung, yaitu alas tabung dan tutup tabung yang berbentuk lingkaran dan selimut tabung yang berbentuk persegi panjang.
Sehingga rumus luas permukaan tabung adalah
Luas permukaan = luas alas + luas tutup + luas selimut berbentuk persegi panjang
Luas permukaan = luas lingkaran + luas lingkaran + luas persegi panjang, dengan panjangnya adalah keliling lingkaran di kalikan dengan lebarnya yaitu tinggi tabung

2. Rumus Volume Tabung
Selain mempunyai luas permukaan, bangun ruang juga pasti mempunyai volume. Tabung merupakan salah satu jenis bangun ruang yang berbentuk prisma tegak yang mempunyai alas dan tutup berbentuk lingkaran. Biasanya bangun ruang yang berbentuk prisma tegak mempunyai volume dengan rumus yang sama, yaitu:
Volume = Luas Alas X Tinggi
Volume tabung mempunyai rumus yang sama mengikuti rumus volume prisma, yaitu
Volume Tabung = Luas Alas X Tinggi
Volume Tabung = Luas Lingkaran X Tinggi
E. Contoh Soal dan Pembahasan
1. Sebuah tabung berdiameter 20 cm dan tinggi 50 cm. Berapakah luas permukaan tabung tersebut?
Penyelesaian:
Diketahui: d = 20 cm maka r = 10 cm
t= 50 cm
Ditanyakan: Luas Permukaan?
Jawab:
Luas Permukaan = 2πr ( r + t )
=2 x 3,24 x 10 (10+50)
=2 x 31,4(60)
=62,8(60)
= 3768
Maka luas permukaan tabung tersebut adalah 3768 cm².
2. Sebuah tangki air yang berbentuk tabung tertutup akan dibuat dengan alas dan tutup yang mempunyai jari-jari 1 meter dan tinggi 70 cm. Berapakah volume air (dalam m³) yang dapat memenuhi tangki air tersebut?
Penyelesaian:
diketahui : r = 1 meter = 100 cm
t= 70 cm
Ditanyakan: Volume air?
Jawab:
Volume air = volume tabung= πr²t
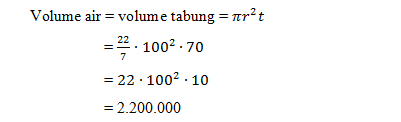
Jadi volume air yang dapat memenuhi tangi tersebut adalah 2.200.000 cm³ atau 2,2 m³.
3. Berapa luas kertas karton yang bisa digunakan untuk membentuk sebuah tempat pensil yang berbentuk seperti gambar dibawah ini?
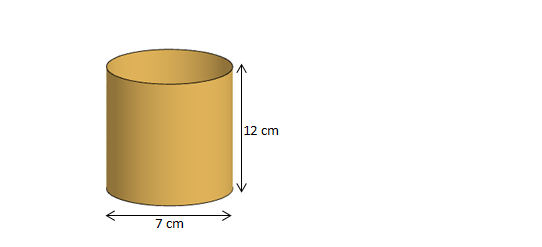
Penyelesaian:
Dari gambar tersebut diketahui bahwa tempat pensil yang akan di buat berbentuk tabung tanpa tutup. Maka untuk mencari luas kertas karton yang bisa digunakan untuk membuat tempat pensil tersebut adalah dengan mencari luas permukaan tabung tanpa tutup.
diketahui : d = 7 cm r = 3,5 cm
t= 12 cm
Ditanyakan: luas kertas karton atau luas permukaan tabung tanpa tutup?
jawab:
Luas permukaan tabung tanpa tutup = πr² + 2 πrt
= πr ( r + 2t )
= 3,14 x 3,5 (3,5 + 2 x 12)
= 10,99 (3,5 + 24)
=10,99 (27,5)
= 302,225
Maka luas kertas karton yang di butuhkan untuk membuat tempat pensil tersebut adalah 302,225 cm².